大家好,我是不会写代码的纯序员——Chunel Feng。上一章内容中,我们跟大家讲解了数据结构中的树,在编码、缓存、数据库等方面的应用例子。这一章,我们再继续这个话题,聊一聊“树”在相似搜索领域和人工智能领域的一些应用。
| 相似搜索领域 |
相似搜索(ANN,Approximate Nearest Neighbor)技术又叫做“向量检索技术”或“相似最近邻搜索技术”,指的是通过单个向量在海量向量中,通过预先设定的索引结构,快速查询出距离(如:欧氏距离、曼哈顿距离等)相近的TopK个向量的方法。该技术被广泛应用于以图搜图,智能问答,搜索推荐系统等领域。
常见的使用场景嘛,比如将海量图片通过embedding技术,生成对应的海量向量集合(Dataset)。然后将查询图片通过同样的方法,得到一个向量(query point),并在Dataset中找到距离最近的n个向量,就可以粗略认定:这n个向量对应的图片,和查询图片比较相似。
K维树(K-Dimension Tree)
我们之前聊过很多树,有的节点中包含一个信息(如:红黑树),有的节点中包含多个信息(如:B树)。还有一种情况,树中的每个节点中,包含一组信息——一个高维向量。这个概念就迎合了上面提到的向量检索了。
KD树是早期做向量检索的方案,建树的时候通过空间内点的方差来确定切分方向、进而再确定出切分点和切分平面,并以此方式递归的对海量向量数据进行切分,直至形成一颗树形结构。
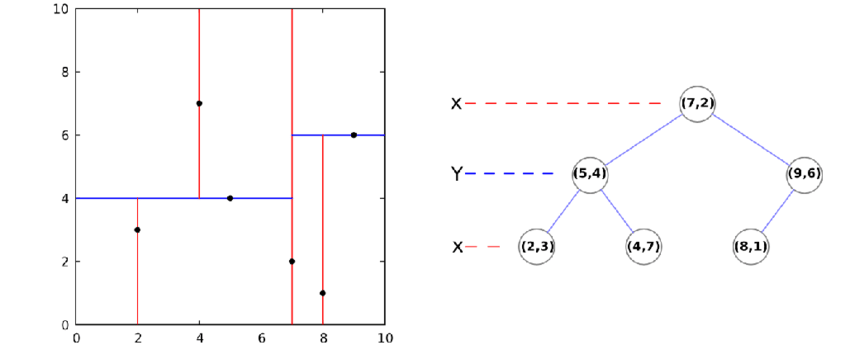
看上面这张图,[2,3] [5,4] [4,7] [7,2] [8,1] [9,6]这几个向量,就被以切面分割的形式,放在了右边的KD树中。查询的时候,根据KD树的路径中的切点和切面信息,通过对比寻址和回溯等流程,最终在海量向量数据中,在减少比对次数的基础上,找到与query点邻近的TopK个点,从而达到加速查询的目的。
Annoy 树
Annoy(Approximate Nearest Neighbors Oh Yeah)算法是Spotify公司开源出来的算法名称,目的和KD Tree一样,也是为了解决海量高维向量的相似搜索的问题。其中也用到的树的思路,而且是多棵树组成的森林。

跟KD树不同的是,它切分的方式是通过对海量向量集合做随机点开始的二值聚类,然后将聚类的索引信息放到根节点的左右两侧(作为“簇”),然后以此方式继续递归,直到每个簇中的节点数量小于特定值为止。这样下来,除了叶子结点以外,所有的路径结点中实际上存储的只是切面的信息,而所有的向量信息均存放在叶子结点中。

这种骚操作是不是有点熟悉,KD树和Annoy树的关系,是不是有点像B树和B+树的关系。需要说明的是,Annoy算法选择起点的时候有一定的随机性,相同的向量集用同样的方法反复多次是会产生不同的Annoy树的。这些树又共同组成了一个描述这批海量向量数据集合的森林。这样做,是为了可以通过多次查询结果合并的方式,提高最终结果的准确率。
类似的技术,还有随机投影树(Random Projection Tree),不过在做平面切分的时候,跟Annoy有所区别。有兴趣的朋友可以深入了解一下,这也是一种通过树(森林)的方式,解决Ann问题的思路。
需要指出的是,目前在相似搜索领域,基于图的算法无论在召回率还是查询耗时层面,都有一定的优势,因此也相对更为主流。但是森林结构有天然的并行属性(因为有多棵不同的树嘛),这是单纯的图结构所不具备的。因而个人觉得这部分今后可能往【图+树】的方向发展。
| 人工智能领域 |
决策树 (Decision Tree)
决策树是一种基于树型结构的、可解释的、有监督的机器学习的方法,而非单纯的一种结构。决策树中的每个非叶子节点均表示一个属性上的判断,而每个叶子结点表示一种分类结果。整体上描述的是算法为了达到特定目标,根据一定的条件而进行选择的过程,被常被用于机器学习中的分类任务。
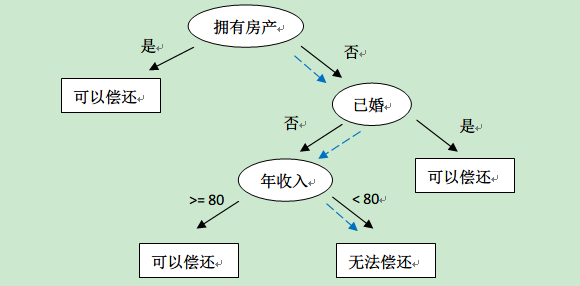
看上面这张图,描述的就是一个根据【是否拥有房产】【是否已婚】【年收入是否超过80(元,嘿嘿,我过了)】这三个(在非叶子节点中)条件来判断借贷人是否有偿还能力(结果在叶子节点中)的一颗决策树。比如,一个没有房产、未婚、年薪低于80的人,会如图中蓝色箭头所示,被判定为无偿还能力。
至于这几个条件中,哪个条件应该被先判断(在树相对顶部的位置),大家可以自行了解一下ID3、C4.5、熵减、信息增益啥的。决策树有着天然的可解释性,在推荐系统中有着广泛应用,有兴趣的朋友还可以了解一下GBDT(Gradient Boosting Decision Tree,渐进残差决策树)。
蒙特卡洛树(Monte Carlo Tree)
蒙特卡洛是摩纳哥一个著名赌城的名字,蒙特卡洛树和游戏、赌(和谐)博等领域能扯上一些关系,常被用于博弈游戏中推测胜出的概率。前阵子大火的AlphaGo,其中就用到的了蒙特卡洛树。
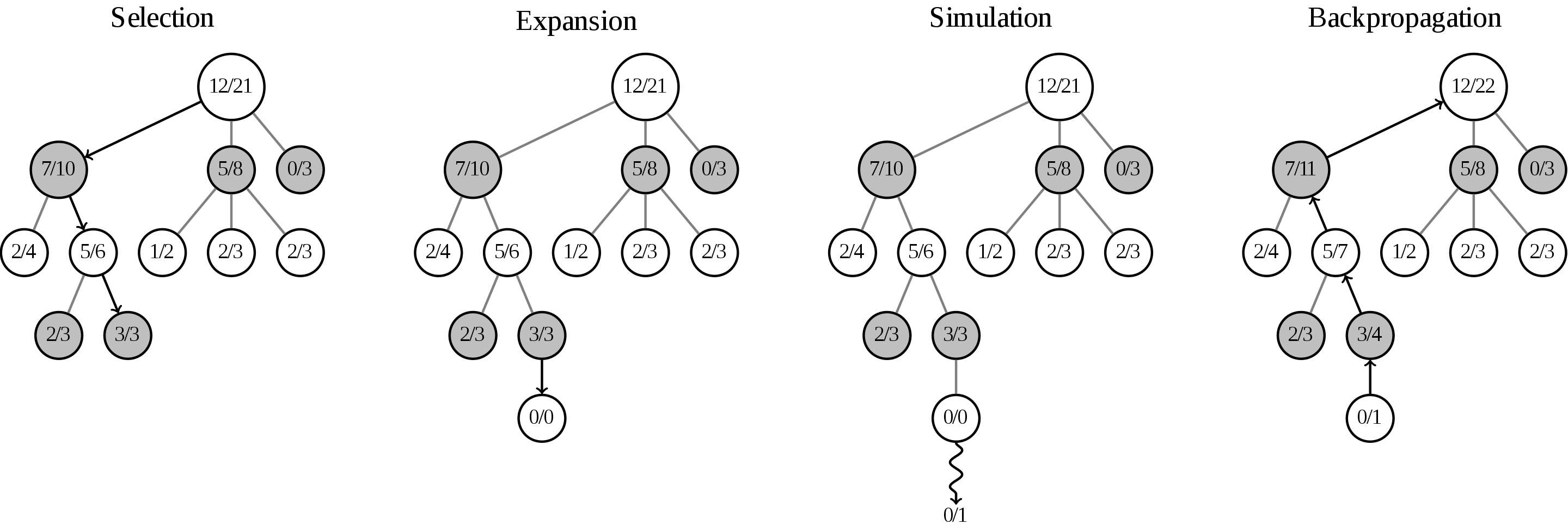
它主要描述的是,通过在设定范围(比如:游戏规则、单步计算耗时等)内,大量反复执行 选择(Selection)、扩展 (expansion)、模拟(Simulation)、回溯(Backpropagation) 这四个流程,逐步的构造出包含了各种可能执行路径,及其对应节点胜出概率的树型结构。
蒙特卡洛树的路径中的每个节点,都表示从当前状态继续进行,可能胜出的概率。而任意节点的子节点,就表示从当前状态出发,至少有几种可选的方案(拿象棋来说吧,就表示,这一步可以把炮向前走三步、或者把卒向前走一步等)。上面的图,可以理解为,经过一系列骚操作后,根节点出发(针对象棋,就理解是当头炮吧),胜出的概率由12/21变化为12/22,从而变的更准确和真实了。
我们刚才聊到了曼哈顿距离、蒙特卡洛树,这些都是以外国城市命名的。
于是,我就去搜索了一下有没有什么内容是以中国的城市命名的。
最后,我学到了一些地产和航空航天方面的知识,比如:蚌埠住了,芜湖起飞。
再简单介绍几种其他领域中常用到的树吧。
默克尔树(Merkle Tree)
默克尔树又叫做 哈希树(Hash Tree),它是将整体内容分成多个区块,然后逐层计算哈希值,并且放入树上的结构。相比于将对分块的哈希值,统一记录到一个Hash Table的做法,默克尔树的主要优势,是它可以分部分进行校验。常用与区块链,密码学等领域。
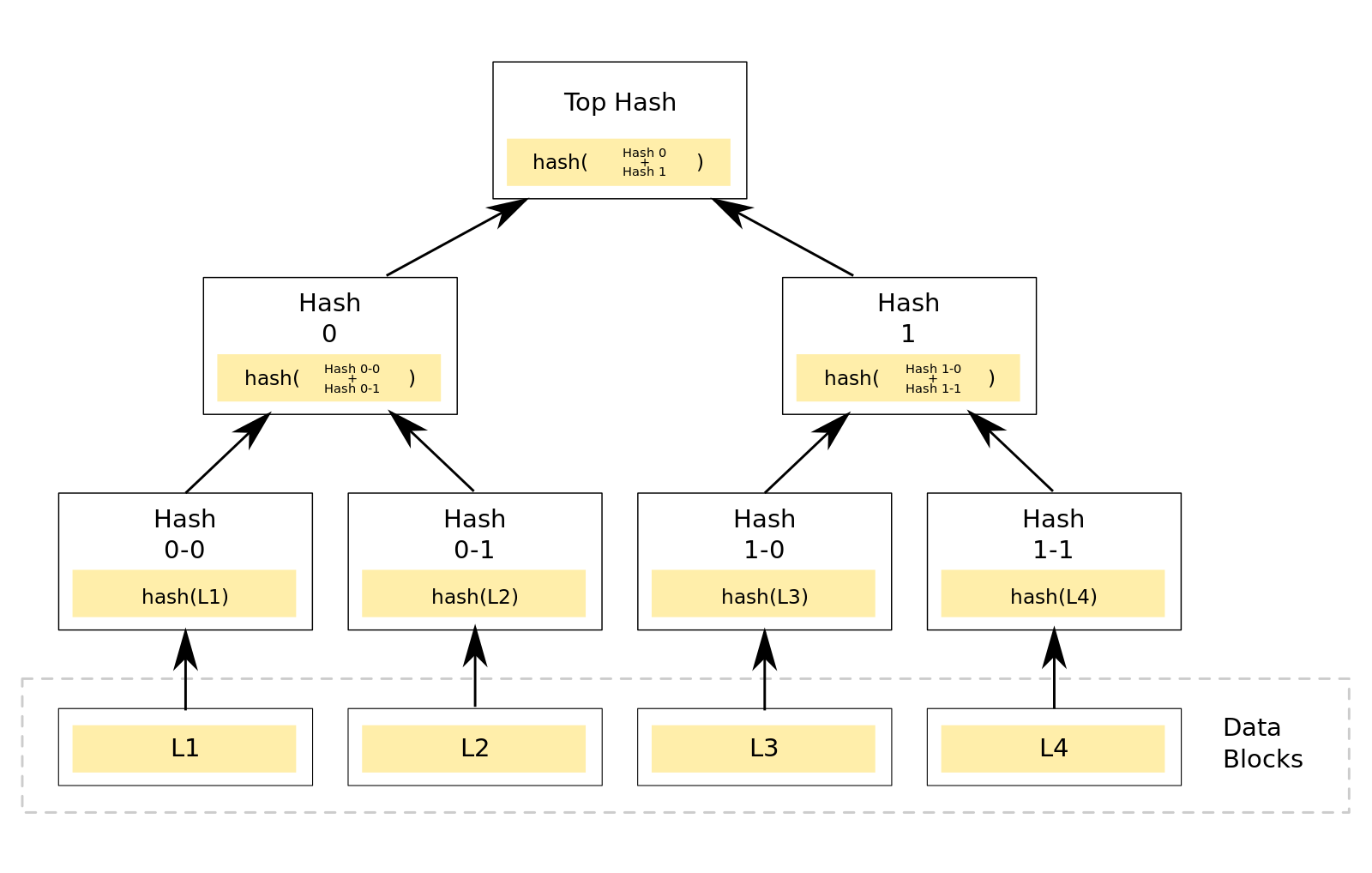
看上面这张图吧,我们可以认为L1(假象为是一个大文件的一个分块)对应的哈希值[Hash 0-0],L2对应的哈希值是[Hash 0-1],而[Hash 0]是对上述两个哈希值(不是分块)再进行哈希后得到的值。这样,在下载文件的时候,如果我想确认前半部分有没有下载完毕,我直接判断已下载部分的[Hash 0]值,跟预期是否一致即可。
当然了,真实的使用场景可能比这复杂了很多。以上说法也是站在一个区块链技术门外汉的角度的进行描述。如果我真的很懂的话,我买的狗币也不会亏那么多了,呜呜。
矩形树(Rectangle Tree)
R树也被叫做空间索引树,可以简单理解为是B/B+树的高阶版本。它的核心思想是通过最小外接矩形的形式,逐层聚合(空间)距离相近的节点。主要应用于地理位置查询等领域,比如在地图上找餐厅这类问题。也被用于数据库领域。
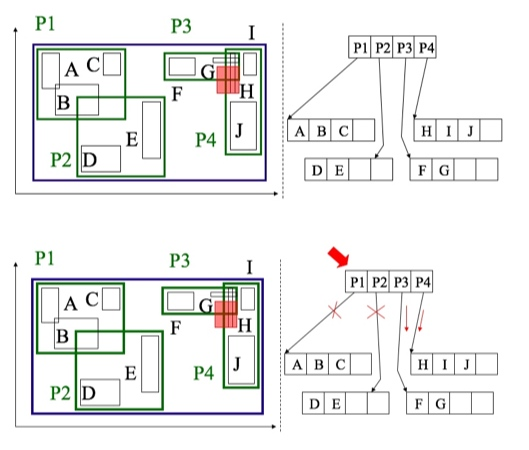
上图是一个二维的R树。图中有10个小分块(可以理解成是餐厅、酒店、娱乐场所等),分别是A~J。它们在R树上根据所在位置,被用绿色的矩形分成了4个部分——分别为P1/P2/P3/P4。如果需要查询红色实心方框附近的娱乐场所,通过在R树上的映射可知,仅搜索P3和P4对应的分块即可,从而减少了查询范围。
相关的内容还有R*树、R+树、Hilbert R树等。有兴趣的朋友可以继续深入研究。
| 本章小节 |
这篇文章是树系列的最后一篇,很高兴能在您的陪伴下,一直写到这里。这几篇文章中,我把我所了解的Tree相关的内容都罗列了一遍,也介绍了这些结构的使用场景和解决的问题。其实,我个人在日常工作中,用到的这方面的知识也不多,像“默克尔树”、“伸展树”这些结构,我也都是最近刚了解的——但,这的确是某些特定细分领域中,最最入门的知识。
这个系列的内容,每一个小节都比较短,也比较浅,希望大家都能看懂并有所收获。今后,如果在特定行业用到了其中某些部分,还需要大家深入了解该结构和其周边的相关知识,毕竟对细分领域知识点了解的深度,才是区别【新手】和【专家】的评判标准。如果,各位专家发现我的表述中,有什么错误、或者不合理、不清楚的地方,也希望不吝赐教。
又想到几年前,我为了找工作,猛刷过一阵子Leetcode。其中很喜欢写的就是树相关的题目——因为简单啊,代码量一般不多,有思路的时候写起来很顺手的。这几年,因为工作原因吧,很久不练,偶尔想写两题的时候,都发现已经很生疏了。
但也是随着工作经验的增长,相比于之前单纯的快速写出某个题目的双优解法,我会更关注一些题目对应的知识点所隐射的内容,比如:
- 它常被用于什么场景?
- 它能用来解决我当前的什么痛点?
- 它能给我接下来的工作,带来怎样的变化?
- 结合手头的任务,我还可以如何去改造和优化它、或者跟哪些内容相结合?
诚然,数据结构和算法的思路,对任何领域的程序员来说,都至关重要。但大家也不用仅仅为了应付一些公司面试,而成为“小镇做题家”吧。必须承认,当前行业环境下,很多人的日常工作中,是基本是用不到这些知识的。双优的题解和答案,总是可以很简单的在网上找到的,但“学有所思”、“学以致用”的能力,更应该是我们在工作和成长的过程中,一点点积攒和沉淀的财富。
我是Chunel Feng,是一个不会写代码的纯序员。感谢您的关注,欢迎添加我的个人微信,随时指教和交流哦。希望我们能一起,用自己的所见、所学和所感,来让世界变得更好——哪怕只有一点点点点。

[2021.11.27 by Chunel]
推荐阅读
个人信息
微信: ChunelFeng
邮箱: chunel@foxmail.com
个人网站:www.chunel.cn
github地址: https://github.com/ChunelFeng
