大家好,我是不会写代码的纯序员——Chunel Feng。在上一章中,我们介绍了6种常见的树结构(BST,AVL,RB Tree,Trie Tree、Radix Tree、Suffix Tree),以及使用场景和解决的问题。是不是感觉hin简单,都把握的住?今天,我们接着聊这个话题,再多介绍几种树。
| 哈夫曼树(Huffman Tree) |
哈夫曼树,又被称为最优二叉树,属于带权值二叉树的一种。它的真实节点全部分布在叶子节点中,是各种可能的组合中WPL值最小的形式(可能不唯一)。
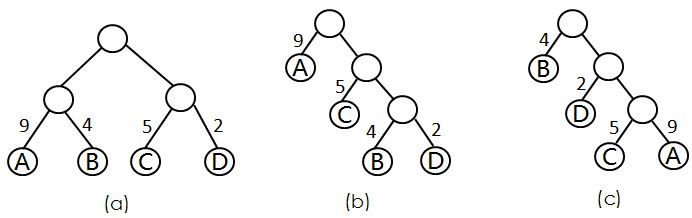
介绍一下WPL(Weighted Path Length),也就是 带权路径长度,说简单一些就是【节点到根节点的路径长度 * 该节点的权值】。说白了就是权值越大的节点,离根节点越近就对了。
WPL_A = 9x2+4x2+5x2+2x2 = 40
WPL_B = 9x1+5x2+4x3+2x3 = 37
WPL_C = 4x1+2x2+5x3+9x3 = 50
看一下上面这章图和三个对应的WPL的值,很明显可以看出来(b)是[9,4,5,2]这几个节点对应的哈夫曼树(的一种表现形式)。我们刚才也提了,哈夫曼树组成的形式可能不唯一,就比如说把(b)镜像过来看,也是哈夫曼树。
哈夫曼树的应用中,最有名的就是哈夫曼编码了。通过这种编码方式,可以使得整体编码的长度最短。还需要说明的是,它是一种前缀编码,任何一个编码值,都不会为其他编码值的前缀(最左子串)。
| 最小生成树(Minimum Spanning Tree) |
最小生成树,虽然叫做“树”,但是它更多的出现在“图”相关的知识中,描述的是将一个有权图,转化成 所有节点均可连通,并且连接边的权值之和最小的树形结构。
提到这个,就肯定要说一下大名鼎鼎的 Prim算法 和 Kruskal算法,这两种算法分别从 随机顶点的角度 和 权值最小的边的角度 出发,一步一步的选出适合的边,然后最终形成一颗包含全部n个节点和n-1条边的最小生成树。对具体流程不了解的朋友,可以自己百度或者B站一下,相关的介绍有很多。
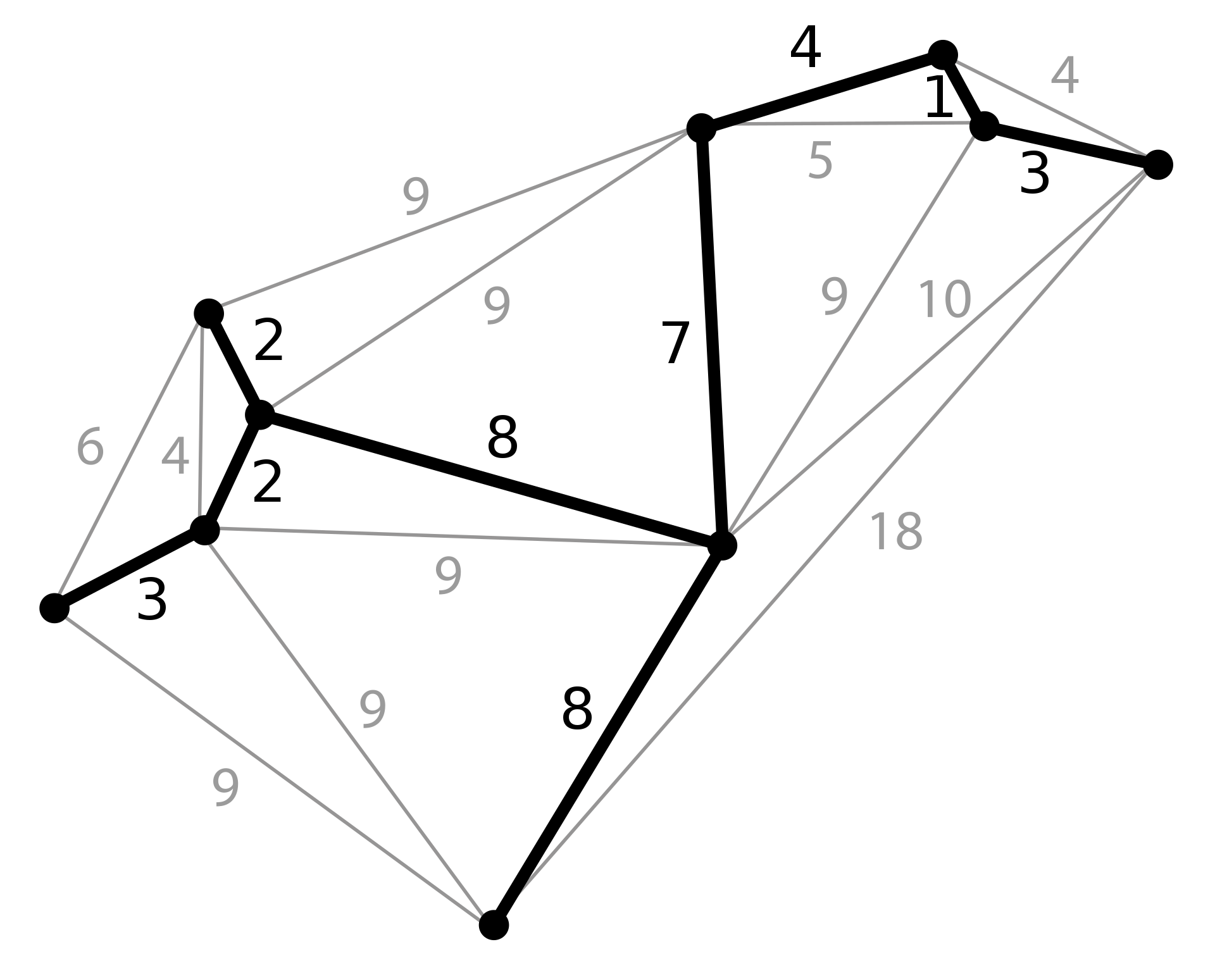
这方面比较经典的应用,就比如多个城市之间建铁路,要求每个城市都连通、并且铁路距离总和最小这种。后来我想想,送外卖的时候兴许也能用到这个方法,可以为35岁之后的职业生涯提前规划起来了。
| 线段树(Segment Tree) |
线段树,是一种特殊的平衡二叉查找树,每个叶子节点表示一个真实的节点信息。而路径上所有的非叶子节点,用来表示它包含的各层级子节点的范围,并用于标记这个范围内的一些信息,比如范围内的max值或sum值等。
线段树可以较好的兼顾区间插入新数据和单点数据修改的逻辑。当更新叶子节点内容的时候,只要更新该节点对应路径上的节点信息即可。主要用于一些对范围查询有很高要求的场景。
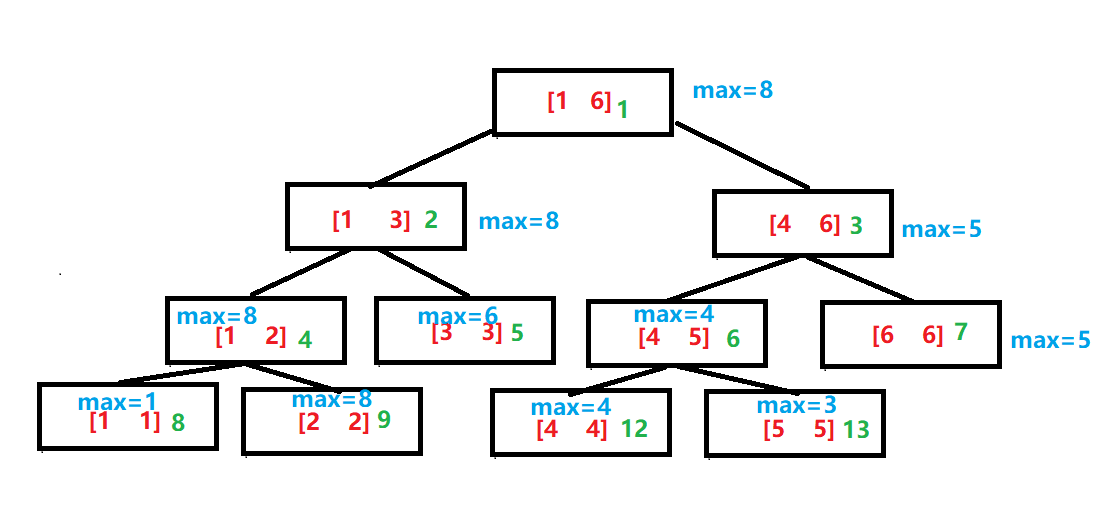
值得一提的是,线段树可以通过一个一维数组来表示,如上图中绿色数字所示(其中10、11为空缺信息)。还需要说明的一点是,类似的概念还有区间树,也有人将这两个概念画了等号,大家自行了解分辨。
| 伸展树(Splay Tree) |
伸展树是一颗非平衡二叉搜索树。它的设计思路,是基于一种假设:最频繁被查询的信息,它(和它附近的节点)在下次查询的时候最可能被查到。所以,相似Splay Tree查询的时候,会随着被查询的信息,反复调整树本身的结构,从而将经常被查询到的节点,放到root附近。这样就可能会加速查询效率。
这个乍一听,有点像LRU或者LFU类似的结构,但是又没有那么绝对。首先,Splay Tree中会保留所有的节点信息,不存在过期(或超限)销毁的情况。还有一点就是它并不是被查到之后立即置顶,会有一些其他的综合考量(比如,每次最多进行n次旋转)。
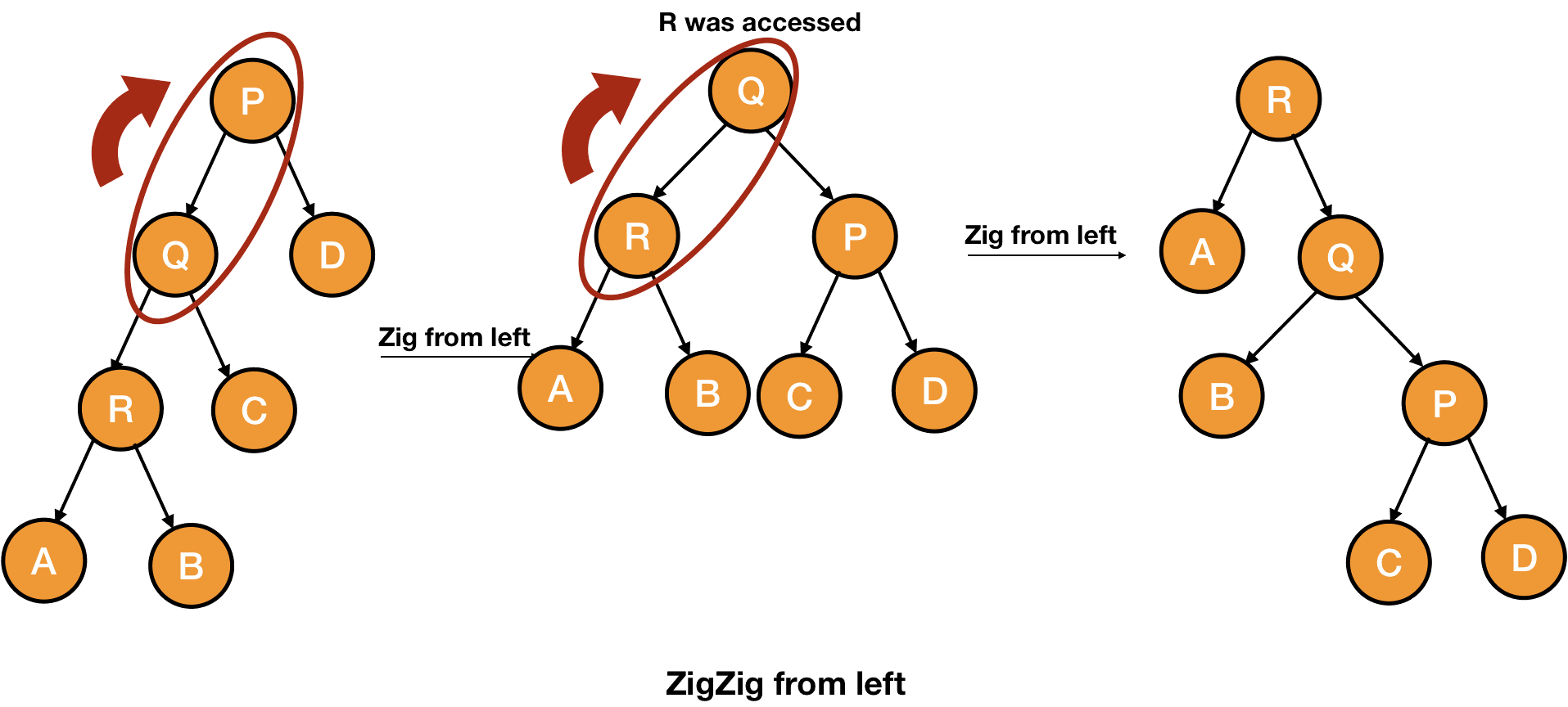
看一下上面这张图吧,它模拟的是(频繁)查询R的时候,Splay Tree的变化情况。说白了就是把R节点放到根节点的位置,下次查起来就方便多了。
Splay Tree比较适合做缓存,特别在热点数据相对集中的情况下,查询效率很高。举个应用的例子吧:我们常用的输入法,当你输入完拼音之后,会根据你的之前选择情况,优先出现某些词语。但很多情况下,又不会直接把你上次选择的词语直接置顶,这就可以理解为是参考了伸缩树的思路。
| 数据库领域 |
数据库中非常核心的一个部分,就是索引结构的设计——这几乎决定了数据库的应用领域。而索引结构的设计,又是数据结构和算法的“重灾区”。下面我们几种来列举几种数据库领域中,常见的树结构。
B树
传统的二叉树中,每个节点中包含一个信息,这样如果节点数比较多,路径就会很深。路径深了,对应的问题就是查询的过程中,需要经过更多的节点,从而造成性能下降。基于此,B树诞生了。
B树也属于一种自平衡树。内部通过分裂机制,能够保持数据的有序。它的单个节点中可以保存2~4个信息。单个节点内部有序,节点之间信息的间隔,可以作为划分下面部分的依据。
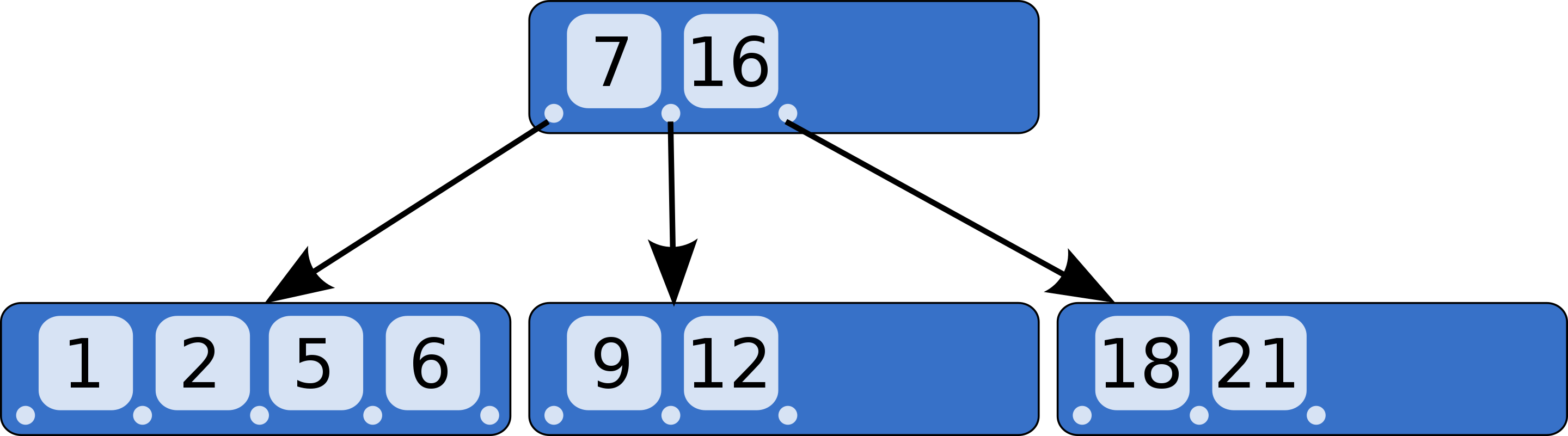
看上面这张图,树中一共有10个信息,按照红黑树的形式存储,最长的路径应该是4。而通过B树进行存储,就会显得“矮胖”了,对应的跨节点查询次数也就缩短了。
B树比较适合于单点查询的场景,比较常见的应用就是MongoDB了。当然了,B树也有一些不适合的场景,比如所有节点都放在磁盘上,则读写性能相对差;再比如说,如果我想查5~9范围内的所有数据,用B树是不是就需要在3个节点中反复横跳?
B+树
B+树就是为了解决上面抛出的两个问题而设计的。与B树相同的是,B+树的节点中也包含了多个信息。但相比于B树,B+树做了一些改动:非叶子节点中仅保留数据之间的相对关系,而所有的真实信息均包含在叶子节点中。这样的话,相对关系信息就可以放到内存中进行存储,将所有节点信息(可以认为量较大)保留在磁盘中。
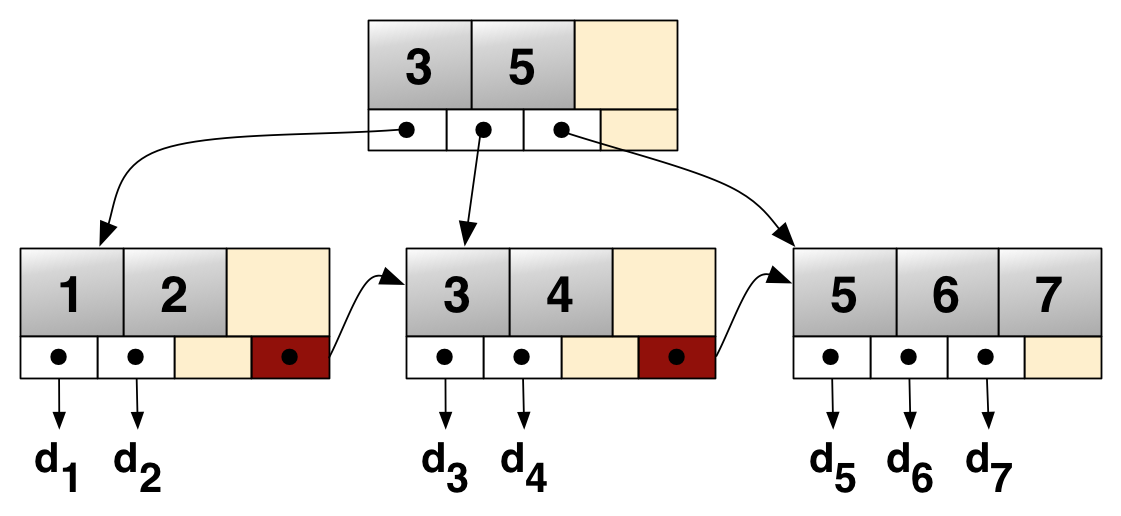
每次查询,通过相对关系,在内存中就可以快速的定位到具体的节点信息,从而减少磁盘的IO次数。这样做还有一个好处,可以通过一条“线”将所有叶子节点串联起来,从而方便做范围查询。大名鼎鼎的Mysql的存储引擎Innodb,使用的就是这种思路。
不知道有没有朋友跟我一样,在很长的一段时间内,把数据库索引和B+树画上了等号。其实不然,不同应用领域的数据库,有着不同的索引结构。B+树的信息存放在磁盘中,且属于非顺序写入,所以查询性能很高,但写入的性能偏低。在大数据存储和日志服务等需要频繁写入操作的领域,就有些不合适了——这就要引出我们接下来的话题了。
日志结构化合并树(Log Structured Merge Tree)
多年前,谷歌在发大据领域发表了Big Table相关论文,LSM树就算是其中的实现思路。我第一次听说LSM Tree,是有幸跟HBase领域的超级大佬一起喝茶的时候聊到的。当时我红着脸表示,只研究过其中的一部分。
与其说它是一种数据结构,其实它更像是基于此思想而衍生出的一系列算法操作的集合。它描述了将实时产生的大批量信息在内存中排序、更新,然后按批次顺序写入磁盘固化、合并的流程,从而兼顾了大批量数据的高效写入存储和范围查询等流程。
我们刚才提到,B+树结构的存储索引并不适合在频繁写入的场景,其中一个很重要的原因就是因为它属于非顺序写入。而针对传统磁盘来说,由于扇区物理结构轮转,顺序写入的性能远好于非顺序写入。
- 随机写入磁盘慢了咋办?
将非顺序的信息在内存中攒成有序的一批信息(Segment),然后一次性写入磁盘不就好了么。
- 攒批的时候,数据丢失或者进程崩溃了咋办?
提前把数据写到一个本地文件(WAL机制)里做备胎(不对,是备份)不就好了。
- 需要在批量数据中做范围查找了咋办?
在内存中记录每个Segment(默认有序)的起止范围,每次查询的时候仅查询范围内的Segment不就好了。
- 数据量太大,磁盘中的Segment太多,影响查询性能了咋办?
当每个Segment大到一定的程度的时候,把几个Segment做归并排序,然后合并到一个大的Segment里不就好了么。
- 写入数据之后,想删除咋办?
根据key找到最后一次写入的信息,打上墓碑记号。查询到的时候,返回没找到不就好了么。
- 墓碑记号太多,占用大量内存,咋办?
- 单点信息查询,数据太多,而且经常miss,咋办?
- 范围查询,不好确认从哪个Segment开始,咋办?
- ...
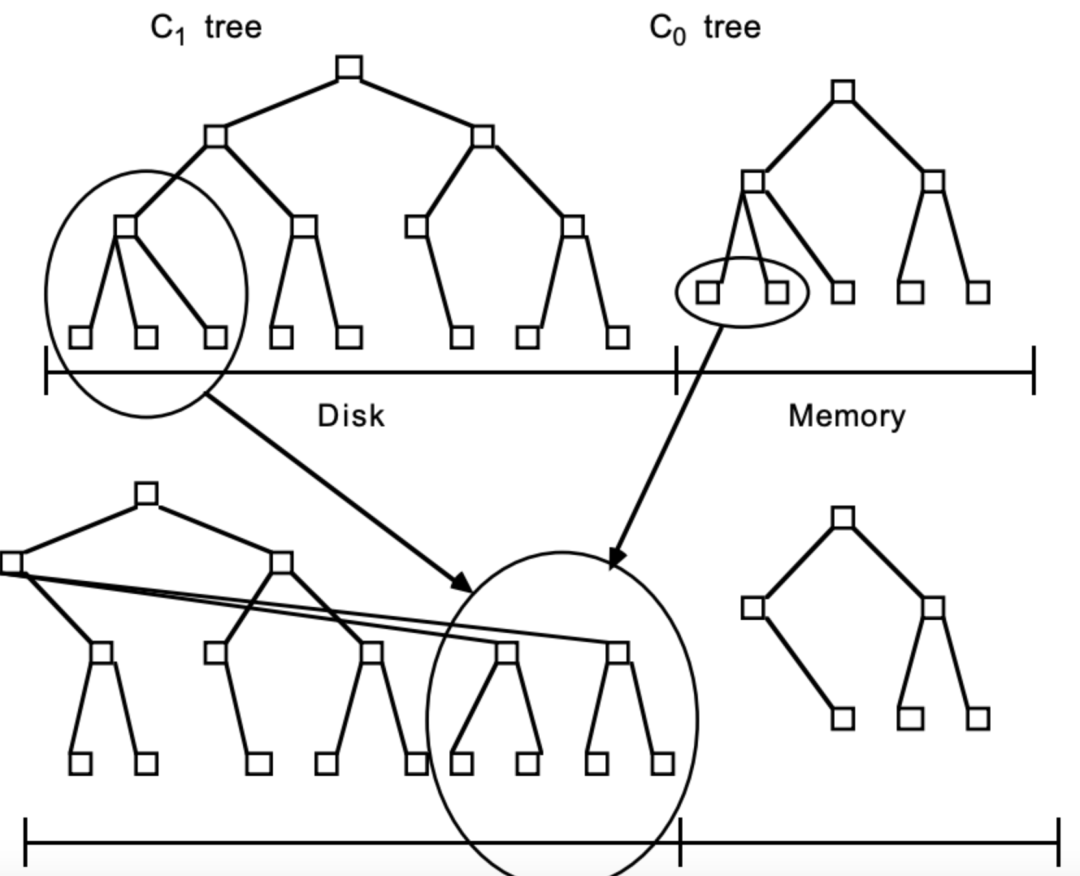
随着大数据的爆火,LSM Tree被广泛用于KV型数据库和OLAP场景中,比如纯序员熟悉(拼写方式)的HBase、Cassandra、LevelDB等。相关领域的问题太多了,同样的,解法也很多,有兴趣的朋友可以深入了解一下。
| 本章小节 |
本章中,我们又介绍了几种常见的树形结构和相关使用场景。旨在说明,Tree在编码、缓存、数据库等领域也有着广泛的应用。特别需要强调的是,在数据库的存储引擎设计方面,Tree可是占据了半壁江山。
那在类似人工智能这种图结构占据主导位置的领域,树结构是否有它的一技之长呢?还有什么行业,会涉及到树结构呢?我们在下一章中,会跟大家继续这个话题。
还是那句话,对这方面感兴趣的朋友,欢迎填加我的微信。彼此交流学习的经验和心得,还可以互相说说段子哦。

[2021.11.20 by Chunel]
推荐阅读
个人信息
微信: ChunelFeng
邮箱: chunel@foxmail.com
个人网站:www.chunel.cn
github地址: https://github.com/ChunelFeng
